Imagemagick Resampling

Introduction

Some of you may be familiar with the blog post I made about mpv's scaling filters a while ago, but it was never really meant to be shared as much as it did. That page was originally the result of an assignment that I had during my undergrad, when I was formally studying digital image processing for the first time. Naturally, it was full of mistakes and the results weren't particularly scientific. I got a lot of feedback and the page ended up evolving in an organic way, but it still has some fundamental issues that can not be fixed without a major change in the methodology.

From the top of my head I can enumerate the following problems:

1. The resampling tests were only done for 1 or 2 test images.
2. I kept adding meme metrics since people requested them.
3. I also kept adding meme shaders since people requested them.
4. I created a bunch of different test cases but didn't really have the motivation to keep all of them up to date.
5. I originally used Matlab to compute the metrics and Excel to plot the tables, which means updating the page was a major pain in the ass.
6. I used catmull-rom in gamma light to downscale the test images.

So, to address these issues:

1. I chose to use the entire Manga109 dataset this time, which is probably the best widely-used dataset we have for line-art.
2. I chose to stick to the standard distortion metrics, I'll think about adding perception metrics to the mix but only if they have decent Python implementations and actually compute at a decent speed.
3. I chose to exclude all meme shaders. I'll stick to resampling filters this time. A following work with meme shaders isn't out of question but this is harder to automate.
4. I chose to only test a few things, don't ask me to add your niche use cases because I won't do it.
5. I chose to automate everything with a Python script so updating the numbers should be trivial (if this is needed at all).
6. I chose to use the box filter in linear light to downsample this time. Since I'm downsampling to 0.5x this should be a simple average of 4 pixels, which is the best case scenario and doesn't introduce any blurriness or ringing.

With that out of the way, we can proceed with the real introduction.

Resampling

Resampling is the process of changing the number of samples of a discrete signal to obtain a new discrete representation of the underlying continuous signal. This definition comes from the idea of having a sensor of some kind producing an analog continuous-time voltage/current variance which is then periodically sampled and quantised into predefined amplitude levels so we can store it in bits/bytes.

The easiest and most classic way of resampling to a higher sample rate is via linear interpolation, if you want to find a value between two points you can simply draw a line between them. Linear interpolation can be done in a cartesian plane, through both axis, creating what we call "bilinear" interpolation. Bilinear interpolation is the simplest interpolation algorithm, the easiest to compute and probably the most widespread one.

But can something as simple as just drawing a line between 2 points give us good results? Sometimes it does, sometimes it doesn't. It really depends on the signal. Instead of taking 2 points and drawing a line, we could take more than 2 points and draw a higher-degree curve. The shape of the curve depends on the weights used in the calculation, and these weights depend on the chosen filter. The number of input samples in the calculation depends on the length/radius/support of the filter. If you want to understand how this is actually done, I suggest simply reading this explanation.

In short, the most common way of resampling images is treating each row/column as an independent 1-D signal and simply going over all of them until you have resampled the entire image. This means you have to choose a dimension to resample first but this is pretty much inconsequential to the end result. The resampling algorithm itself is pretty simple, for each output sample you simply centralise the filter on top of it and see which input samples end up inside of the window after you compute their equivalent positions, then you multiply these inputs by their corresponding weights depending on their distance to the centre.

There's a different method, usually called polar/cylindrical/elliptical resampling, that does the operation in the 2-D domain directly. The only difference here is that all samples that fit inside the 2-D filter will now be weighted simultaenously, which may drastically change how some filters behave since we're only calling the filter once per output pixel rather than twice as before.

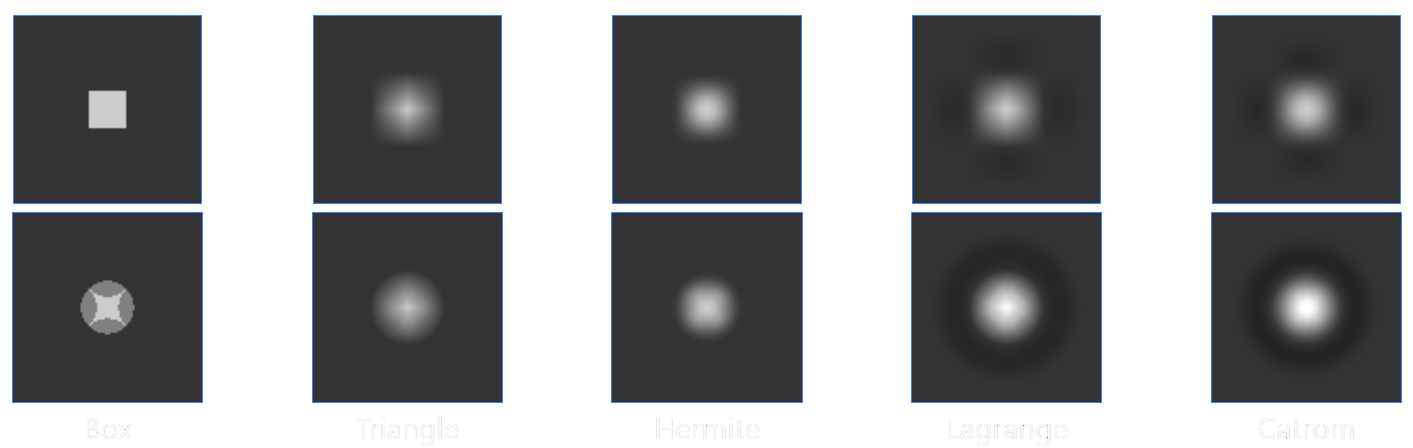
In this page I'll include results for both orthogonal and polar resampling. It's important to note that polar resampling implementations are generally slower and most filters weren't really designed to be used in this way (the most "famous" exception being polar lanczos, since we replace the sinc function with its 2-D "equivalent", the jinc/sombrero function).

Upsampling Methodology

As stated before the entire Manga109 dataset will be used in this comparison. This dataset has manga covers that look like this:

The dataset is downscaled with:

The dataset is then brought back up with the following command for orthogonal resampling:

And the following command for polar resampling:

The {resampling_filter} argument is replaced by all available resampling filters: ['Bartlett', 'Blackman', 'Bohman', 'Box', 'Catrom', 'Cosine', 'Cubic', 'Gaussian', 'Hamming', 'Hann', 'Hermite', 'Jinc', 'Kaiser', 'Lagrange', 'Lanczos', 'Lanczos2', 'Lanczos2Sharp', 'LanczosRadius', 'LanczosSharp', 'Mitchell', 'Parzen', 'Point', 'Quadratic', 'Robidoux', 'RobidouxSharp', 'Sinc', 'SincFast', 'Spline', 'CubicSpline', 'Triangle', 'Welch']

For a much better explanation of these filters, please check this page from Imagemagick.

The result is then evaluated with MAE, PSNR, SSIM and MS-SSIM. All calculations are done with all three RGB channels and in double-precision floating-point for accuracy. Metrics are normalised between [0, 1] and then averaged together with a normal arithmetic mean.

Please note that some of those filters are just aliases to other filters or aliases to sinc/jinc with different windows.

LanczosRadius is supposed to be a jinc-windowed jinc sharpened to have its third zero crossing at 3 instead of 3.2383154841662362.

LanczosSharp and Lanczos2Sharp are both supposed to be sharper jinc-windowed jincs since the original filters ended up too soft when compared to their sinc-windowed sinc orthogonal equivalents.

Upsampling Results

Upsampling Commentary

We started this little adventure to provide a bit more robustness to the numbers compared to my previous comparison done using mpv, and there are a few surprises in the results. The first one is that orthogonal LanczosSharp ended up on top of the table, an option that shouldn't even be in the comparison. If you want to give it a try on mpv, you can use --scale=lanczos --scale-blur=0.9812505644269356.

The second surprise is that Polar_Catrom is at the second place with the best scores for both SSIM and MS-SSIM. Polar_Catrom is an extremely sharp filter, albeit with too much aliasing and ringing. Since it only rings once (when it overshoots), it's trivial to remove all ringing if we just clip the output of each pixel to the limits set by the surrounding input pixels. I have actually written a shader for it, but you can also just use libplacebo's native AR now. If you want to give the filter a try on mpv, you can use --scale=ewa_robidoux --scale-param1=0 --scale-param2=0.5.

The third surprise is that there are some Lanczos variants on top of the baseline Lanczos: Hamming, Cosine and Welch. For the last two all you gotta do is set --scale=lanczos --scale-window=window, but for the first you also have to set --scale-radius=4.

Finally, it's also a little bit funny to see Lanczos2 beating Catmull_Rom in the "orthogonal filters with radius = 2" category. And it's even funnier that Lanczos2Sharp beat them both, another filter that shouldn't even be here. To use Lanczos2 on mpv you can simply do --scale=lanczos --scale-radius=2, and for Lanczos2Sharp add --scale-blur=0.9549963639785485.

You might have also noticed that Polar_LanczosRadius is on top of Polar_LanczosSharp. Polar_LanczosRadius is sharpened to have its third zero crossing exactly at 3, which corresponds to a blur factor of 0.9264075766146068 (3.0/3.2383154841662362). To try it on mpv you can use --scale=ewa_lanczos --scale-blur=0.9264075766146068. On --vo=gpu you also have to specify --scale-radius=3.2383154841662362.

Overall it looks like the filters were more or less ranked from sharpest to softest. This makes perfect sense as the main problem with image upsampling is unintended blurriness. PSNR is calculated using the MSE so it's overly sensitive to outliers, which naturally end up being the sharp transitions. SSIM was also literally designed to give good scores to distorted images that have similarish structures, which also favours sharpness. MAE is a little more neutral than PSNR which is why we generally use it as our target when training distortion-based CNNs, so it should punish filters that are too sharp in detriment to ringing, aliasing and blocking. That's the main reason why most of those CNNs end up generating images that look like oil painting. MS-SSIM was added to neutralise stupidly minor differences as we wouldn't be able to see them anyway from normal viewing distances.

As usual, the filters are ranked based on full-reference distortion metrics that may not always correlate with the human perception of quality, and your personal preference is entirely subjective.

Please also keep in mind that only the named filters were "benchmarked", but you can make "custom" filters that score even higher using the expert controls.

Downsampling Methodology

The problem with downsampling evaluation is that we do not have a "ground truth" image, making it impossible for us to use the standard full-reference quality metrics. However, in the previous section I already made the concession that, at a 0.5x scaling ratio, the box filter is as good as it gets without producing any artifacts.

If we make the leap of faith that resampling filters will more or less keep their character regardless of scaling factor, we can use the output of box as the reference and compare other filters against it. So, in short, we want to find a filter that, at any scaling factor, will behave similarly to box at 0.5x. I'm calling this a leap of faith because this hypothesis most likely falls apart with extreme scaling factors, but as long as you keep it close to 0.5x it probably makes sense.

With that said, now we can proceed to the actual methodology. The reference is created with:

The dataset is then brought downscaled with the following command for orthogonal resampling:

And the following command for polar resampling:

The {resampling_filter} argument is replaced by all available resampling filters. Everything else about the process stays the same, so we can proceed to the results.

Downsampling Results

Downsampling Commentary

The results were relatively predictable, but there are a few things worth mentioning. The first one is that this methodology seems to really like filters with only 1 or 2 lobes. Lanczos2Sharp (--dscale=lanczos --dscale-radius=2 --dscale-blur=0.9549963639785485) takes the podium but the other BC-Splines and the normal Lanczos2 aren't far behind.

It's a bit funny to see Polar_Hermite (--dscale=ewa_robidoux --dscale-param1=0 --dscale-param2=0) so high in the list, but I actually think it makes sense. Hermite is a short (radius 1) filter that does not have any negative sections, so using it to downscale makes the operation very close to an "area average", the only difference is that pixels are weighted based on distance. Hermite is usually described as a "smooth" triangle, but it scores much higher than the "normal" triangle.

It's also interesting to see that Polar_Robidoux wasn't the best polar BC-Spline, considering the filter was specifically designed to be good at -distort. In any case, it's only slightly behind Polar_Mitchell. Please remember that these BC-splines are all sharper when used in polar resampling, so Polar_Mitchell is actually a pretty sharp filter and a relatively good alternative to Catrom if you prefer the look of polar resampling.

Both Lanczos (orthogonal sinc-sinc) and Polar_Lanczos (polar jinc-jinc) were pretty mediocre at best. That's a good thing because it shows the methodology can actually punish filters that are too sharp. Polar_Catrom, the sharpest filter we have in the comparison, actually scored as one of the worst filters.

I think this test solidifies what was already common knowledge. BC-Splines are very good at downsampling, and pretty much all of them are near the top.

Outro

Nicolas Robidoux has a personal page with some recommendations, if you want a more qualitative approach.